|
每年NMOS试题有30题,其中大部分题目拼的是熟练度,少部分难题就得拼硬实力了。以下是2006年至2021年NMOS中难题的分布情况: 从图中可以看出,计数问题在难题中的出现频次是最高的,想考高分,计数问题得牢牢吃透!今天给大家讲讲NMOS试题中的最难的几类计数问题。
一、排列计数问题 先看一道真题: (NMOS 2017R1 Q30) A 4-digitnumber is formed by using the integers only once in the list {1, 3,4, 6, 8, 9} Forexample, 1348, 3691 and 4896 are possible numbers but 1234 and 3344 are not. If the numbers are arrangedfrom the smallest to the biggest, which position would thenumber 4386 be in? 本题给了数,让我们求具体的位置,下面给出详解: 小于4386的四位数,首位必然是1或3或4。 首位为1或3时,其他数位可以随便填,首位有2种,其他三个数位分别有5、4、3种,共2×5×4×3=120个。 首位为4时,百位只能为1或3。若百位为1,则十位和个位分别有4、3种,有4×3=12个,若百位为3,则十位和个位可以为16、18、19、61、68、69、81,共7个。 至此,所有小于4386的四位数共120+12+7=139个,故4386排在第140个位置。 此方法的关键:将数列中的数根据排列规律进行分类,每一类单独计算!
利用这种思想,我们快速解决另一道“第29题”: (NMOS 2009R1 Q29) Kevin wrote whole numbers starting from 1. Then he put a “#” behindevery 3 digits as follows: 1 2 3 # 4 5 6 # 7 8 9 # 1 0 1 # 1 1 2 # 1 3 1 # ... What is thedigit before the 100th “#”? 与之前相反,本题给了具体的位置,反过来求数,但思想是共通的: 首先,第100个“#”前的数字应当是这个数列中的第300个数字。 我们根据每个多位数占据的位置个数进行分类: 一位数:1~9,共9个位置 二位数:10~99,共2×90=180个位置 三位数:剩余300-180-9=111个位置,相当于111÷3=37个三位数。 如此相当于刚好写完了99+37=136,所以第100个“#”前面的数字是6。
所以这类排列计数问题,关键是根据数列的排列规律分类。分类恰当,就能轻松解决
二、反面考虑思想 先看一道真题: (NMOS 2009R1 Q29) How many whole numbers from 1 to 2009 contain the digit “2”? 题目意思非常明确,但是如果仔细想想1~2009中包含数字“2”的情况,会发现实际情况很复杂:有几个数字2? 数字2出现在哪些位置? 分类情况很多,计算难度很大。 所以包含2,是很复杂的,我们可以从反面考虑——先算出不包含2的,再从所有情况中减去即可。 不包含2即相当于1~1999,这里再使用一个技巧——数位扩充:把不足4位的数左边补0,使之变成4个数位,比如1可写成0001,45可写成0045。 这样,1~1999中没有2的数,从左往右第1个数位可填0或1,后3个数位除了2都可以填,共2×9×9×9=1458个 但这里面包含了0000,需要减去1,所以共有1457个数是不包含2的,那么包含数字2的就有2009-1457=552个数。 本题关键:正面讨论比较复杂,就从反面考虑,最后从整体减去。数位不足可添0扩充数位。 下面是NMOS官方的参考解析,采用分段计数,足以说明正面考虑太复杂:
三、数三角形问题 NMOS中数图形问题考得比较多,其中最难的就是数三角形,这里给大家介绍一种数三角形的“万能解法”。 来看真题: (NMOS 2018R1 Q16) Find the total number of triangles in the figure shownbelow.
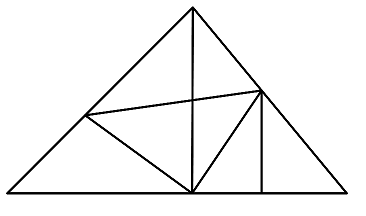
本题的一种解法是按照组成三角形的区域块数分类枚举,但是要做到不重不漏很有难度,而且如果图更复杂一些,就几乎不可能通过这种方法解决了。 我们可以先把这个图简化一下:
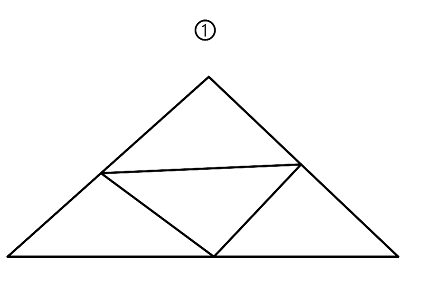
①图中,别忘了整个的大三角形,共有5个三角形。
接下来我们加一条线:
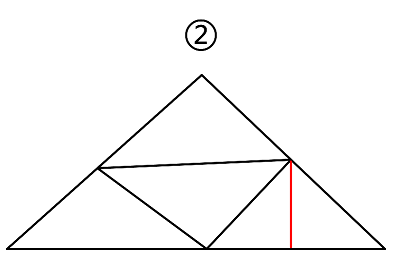
②图相比①图新增了一条线,那么新增的三角形将全部由新增的线带来。 对于新增的这条线,实际上还需再找1个点,才能形成三角形。
从图中每个点出发,与红线能组成三角形的只有2个点,每个点分别可形成1个三角形:
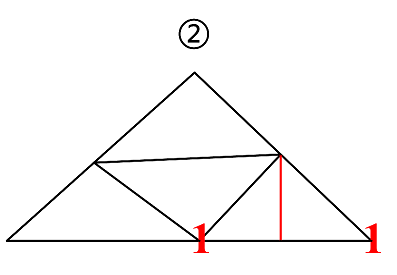
所以目前共有5+2=7个三角形。
接下来我们再加最后一条线:
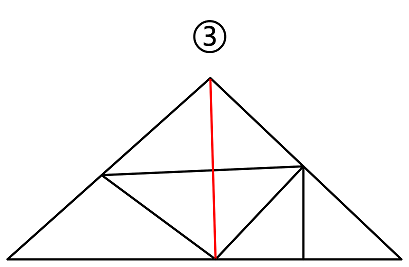
③图中,出现了这种情况:
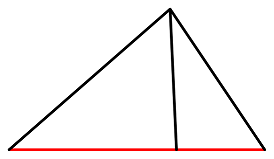
此时上方顶点可与下方红线组成3个三角形。
将每个点对应新增的三角形标出:
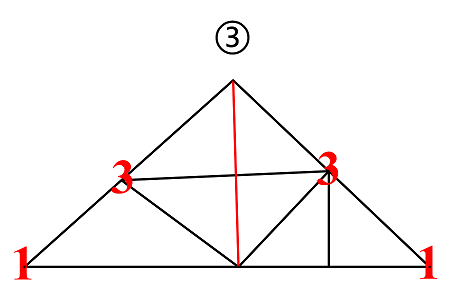
所以原题中共有7+1+3+1+3=15个三角形。 本题关键:先将图形简化到可轻易数出的情形,然后再1条1条线地增加,每次把新增的三角形累加,这叫增线法。 显然,增线法使用熟练后,解决比较难的数三角形问题可游刃有余!
对于本身基础还不错的同学而言,NMOS一试肯定是奔着满分去的,所以简单题熟练度要高,而难题的解题方法也需要知晓并能熟练运用。本帖介绍了NMOS计数问题中最难的3种类型,希望大家有所收获~ 老师也出了几道题给各位同学,学到技巧后赶紧动手尝试吧~同学们回复到本帖中,我会回复的哦!
Question 1: A 4-digitnumber is formed by using the integers from 0 to 9 only once. For example, 1028,3691 and 9281 are possible numbers but 1134 and 8010are not. If the numbers are arranged from the smallest to the biggest, which position would the number 2345be in? 用0到9这十个数字组成没有重复数字的四位数;若将这些四位数按从小到大的顺序排列,则2345是第几个数?
Question 2:How many three-digit numbers can beadded to 786 with at least one carry? 与786相加至少产生1次进位的三位数有多少个?
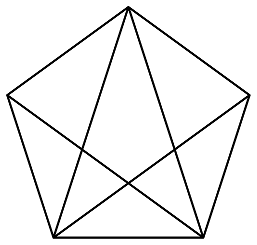
Question 3:Findthe total number of triangles in the figure shown below. 下图中共有几个三角形?
|