|
S1重难点分析及解决方案 如图,是S1阶段所有章节的知识点,数与代数,几何,统计都处于刚起步的阶段, 知识点相对比较简单。但其作为各大模块的基石,中一数学的扎实程度决定了未来数学的成绩。很多同学在学校里的学习中感受不到压力,慢慢积累了很多小问题,这些问题在进入中二中三,遇到困难(如学科的增加、难度的加深)后,就凸现出来。并且根据往届的学生的反馈,O-Level中E-Math要拿到A1需要85~90%+,A-Math也需要80~85%+,与公布的75%+是有较大差距的。所以不能被中一校内成绩的A1所麻痹了,而且年级升高,难度升高,拿高分会越来越难。所以中一数学,我们的目标至少是90+,乃至100分。 | Chapter | | | Primes, Highest Common Factor and Lowest Common Multiple | | Integers, Rational Numbers and Real Numbers | | Approximation and Estimation | | Basic Algebra and Algebraic Manipulation | | Linear Equations and Simple Inequalities | | Linear Function and Graphs | | | | | | Ratio, Rate, Time and Speed | | | | Triangles, Quadrilaterals and Polygons | | Geometrical Constructions | | Perimeter and Area of Plane Figures | | Volume and Surface Area of Prisms and Cylinders | | Statistical Data Handling |
在中一数学中的重点和难点主要集中在“有理数与实数”,“代数式与方程”,“一次函数与图像”,“平行线与基本图形”下面针对上半年刚进入中学的重点给大家提供一些分析与资料分享。 (1)重点知识1:有理数与实数的计算
计算永远是数学的基础,小学升入中学最重要的一个变化就是数系进一步拓展到了负数,有理数,实数,这使得计算的复杂程度大大增加。如下面例子,小学需要掌握整数,小数与分数的加减乘除,而中一计算计算的复制程度显著增加,尤其是在“复杂混合运算”,“符号的变化”,“乘方的运算”时,诸如
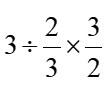
等于3吗?
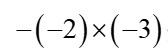
是正是负?
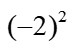
和
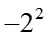
有什么区别?这些看似简单的问题,对于刚接触的孩子来说并没有那么简单, 出错率特别高。只有解决了计算问题,才能学好后续学习代数式运算。 计算问题的解决主要分两步: 一是要理解计算的本质逻辑,做好方法总结;二是通过练习提高熟练度。为此,之前给同学们发过《计算420题》,大家可以每天定时定量进行练习,及时订正总结,坚持一段时间就会有显著进步。如果还有需要的同学可以联系我领取。 (2)重点知识2:代数式与方程 小学侧重对数本身的理解与运算,重点使用“Model法“,但中学更强调代数方法的熟练应用。以一个题目为例: | PSLE 2021 Q15 | O-Level 2022 E-Math Paper2 Q10 | Helen and Ivan have the same total number of coins. Helen has a number of fifty-cent coins and 64 twenty-cent coins. The total mass of her coins is 1.134 kg. Ivan has a number of fifty-cent coins and 104 twenty-cent coins. (a) Who has more money in coins? How much more? (b) Each fifty-cent coin is 2.7 g heavier than each twenty-cent coin. What is the total mass of Ivan's coins in kg? | A small business makes jewellery. Workers are paid a basic hourly rate with an additional payment for each item they make. These are the employment guidelines provided for the workers. | Total of 40 hours per week over 5 days 18 days annual holiday paid at basic hourly rate Expected annual income at least $48 000 |
(c) In one day, a total of 132 necklaces are made. Chen and Zhu make these necklaces. Zhu takes 80 seconds less than Chen does to make each necklace. They each work for 8 hours a day. Can Chen and Zhu each expect to earn the advertised minimum annual income? Justify your decision and show your method clearly. [8 Marks] |
左边是大家讨论的PSLE近10年来最难的题目,关键点是找到“差量”, 如下,用“Model法”画好图就很好解决了。但是“Model法”是有局限性的,他只能解决“加、减、乘”等运算关系,无法处理“除法(分式)、高次”等复杂关系。 所以中学的题目“代数”是核心方法,比如右图则是22年O-Level中学生反馈较难的一个,需要列“分式方程”。 中一起步,我们会学习代数式的化简,简单的因式分解,分式与方程。这些都是未来学习函数,微积分,几何与三角函数等的基础。 为此,本文末尾给大家准备了一份《代数与方程》手册,里面详细列举了中一阶段代数与方程中的重要概念与例题展示,以及O-Level等考试真题与拓展题型。大家可以下载学习,存在疑惑的可以联系老师解答。 根据多年的教学经验,发现大部分同学在学习都存在以下问题: 1、对知识点的理解浮于表面; 2、解题没有技巧,每次做题都像是做新的知识,缺乏举一反三的能力; 3、小错误不断,同样的问题一错再错,始终不能完整的解决问题; 4、不求甚解,问题越积越多,导致跟不上学习节奏。 5、解题效率低下,无法在规定的时间内完成试卷; 以上问题与习惯的培养都要在中一解决,否则进入中二、中三,知识点上的增多和难度的增加,同学们可能就会出现成绩的滑坡。 针对这些问题,大家需要重视一下几点: (1)重视概念和公式的理解和记忆 如果只顾做题,忽视了概念的理解。就容易导致理解不了题目,方法记不住。比如学习LCM和HCF时,divide和divided by是不一样的,再比如一次函数的解析式的构成,斜率和截距,不理解其概念与意义,每次做题都想不起来方法。先理解,再记忆,这是学好的基础。 (2)做好题型特征与方法的总结 题目不是做的越多越好,对于频繁出现的题型与知识点,要针对题目的特征与方法进行分类总结,比如因式分解,中一只学一个方法,就是提取公因数,公因数可以是“数”,“字母”,“括号(括起来的一个整体)”,总结好后做题就按照这个顺序去找。不管题目怎么变,我们都会有思路。否则就会陷入每天做重复,相似的题目反复做,却没有进步与提升。 (3)重视每一道错题的反思与整理 一定量的刷题练习是必要的,一是将所学的知识点和技巧,在实际的题目中演练,增强理解。二是从中找出自己的不足,查漏补缺。所以错题很重要,不管是做错的还是完全不会做的,都要想办法弄懂,做好错因与方法总结,并定时重做。否则很容易沉浸在大量做题产生的虚无的成就感中,很累但是没有意义。 (4)遇到问题,及时提问请教。 知识本身是有连贯性的,前面的知识不清楚,学到后面时,会更难理解。当问题积累到一定程度,就会造成你对该学科慢慢失去兴趣。直到无法赶上步伐。所以一定要杜绝“不求甚解”,“羞于提问”的想法。“打破砂锅问到底”的精神才是老师鼓励的。 (5)注重考试经验的培养 有的同学平时学习很好,作业正确率很高,可一到考试,成绩就不理想。这种现象,主要有主要原因:一是考试心态不不好,容易紧张;二是,考试时间紧,规定时间内完成不了。考试心态可以多参加大型正式的考试,找到调整自己心态的合适方法。做题速度慢则要注重平时的练习。限时定量,逐步提高熟练度与效率,同时多思考题目的不同解法,寻求最佳解法。 大家在中一注重以上习惯的养成,并陪以科学,系统的学习与练习,大家一定能取得理想的成绩。我们一起加油,有什么问题可以和我反馈。
|