一文搞懂2024 APMOPS考了三次的方法——插板法

崔老师

NMOS结束后我们要开始备考明年的RMO和APMOPS。而计数问题一直是APMOPS中的重难点知识，

其中“插板法”是这一模块中的常考方法，尤其是在2024年APMOPS中，有三道题目都是用“插板法”解决，三道题考同一个知识在任何一个竞赛中都是非常少见的情况，那到底什么是插板法？如何用插板法来解决计数问题呢？这一篇文章将会把它讲懂讲透。

一、什么是插板法？

理解插板法之前我们先来思考一下以下问题：

把4个相同的苹果分给A、B、C三位小朋友，要求每位小朋友至少分得1个苹果，共有多少种不同的分配方法？

常规解题思路：通常人们会用枚举法解决这个问题：4=1+1+2, 4=1+2+1, 4=2+1+1，可以得到共有三种分配方式，但这个方法有个局限性：如果要求分配的苹果数量很多，那枚举会花大量的时间且容易出错。在此基础上，数学家们想到了另外一种解决问题的思路——插板法。

插板法解题思路：4个苹果摆放成1排，如果想要分给从左到右A、B、C三位小朋友，那么只需要将苹果用2个木板隔成三堆，如下图：

圆圈代表苹果，竖线代表木板，所以从左到右A获得1个苹果，B获得1个苹果，C获得2个苹果，于是这个“分苹果”的问题就变成了找空隙“放木板”的问题，我们可以发现4个苹果之间会有3个空隙，只需要选择两个空隙放木板即可，那么可以用 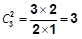来计算，在此方法下，不论多少个苹果分给多少位小朋友，我们都转化成“插木板”解决，比如把20个相同的苹果分给5位小朋友，要求每位小朋友至少分得1个苹果，用插板法我们可以知道，20个苹果共有19个空隙，分给5位小朋友需要插4个木板，所以共有 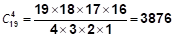种分配方法。

二、插板法的局限性

数学家们在发明了插板法后在欣喜的同时也发现了它的局限性——只能解决“至少拿1”的问题。即在苹果空隙中放木板，则分成的每堆苹果中至少都会有1个苹果，那么如果把上述问题更改下，变成下述两类问题：

（1）至少为0：

把4个相同的苹果分给A、B、C三位小朋友，要求每位小朋友至少分得0个苹果，共有多少种不同的分配方法？

那么应该如何解决呢？

这时就要用奥数中常见的解题思路：未知问题转化成已知问题——我们已经学会“至少为1”，如何将“至少为0”变为“至少为1”，做法非常简单，我们只需要再借3个苹果分给A、B、C一人一个，那么剩下的4给苹果不管如何去分，每个人拿到的苹果数量都是“至少为1”的，此时我们就将“4个苹果分3人至少为0”变为了“7个苹果分3人至少为1”，那么就可以用刚刚的插板法来解决了：

如上图是7个苹果A分1个、B分1个、C分5个的情况，将借来的苹果还回去就可以得到A分0个、B分0个、C分4个的情况，由此一一对应，可得所有的分配方法共有 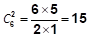种。所以“m个苹果分给n个人，要求每个人至少为0“，就可以通过借苹果变成“（m+n）个苹果分给n个人，要求每个人至少为1”来解决问题。

（2）至少为a：

把10个相同的苹果分给A、B、C三位小朋友，要求每位小朋友至少分得3个苹果，共有多少种不同的分配方法？

上述问题变成每个小朋友至少分3个苹果，应该如何解决呢？

聪明的你应该已经想到了，还是同样思路，将未知问题转化成已知问题：我们只需要先给每个小朋友分2个苹果，这样之后剩下的4个苹果，再按照每个小朋友至少分1个来分配。这样就可以实现每个小朋友至少分得3给苹果，所以“m个苹果分给n个人，要求每个人至少为a”，可以通过每人先分a-1个苹果，变成“剩下的苹果分给n个人，要求每个人至少为1”来解决问题。

三、插板法的常见变形

通过学习上述第二部分，我们就可以解决任意数量的“苹果“分配给小朋友的问题，但在考试中此类题目会有一些变形。

（1）分“苹果”变成分“万物”

插板法能够分的对象不仅仅局限于物品，例如2020年APMOPS的第29题：

29. How many different ways are there to express10000 as the product of 3 positive integers?

(Note: Order is important, for example, 1×100×100 and 100×1×100 are considered twodifferent ways.)

这道题我们发现我们要做的实际上是把10000分成3个数，更加本质来看是把2的4次方（4个2）和5的4次方（4个5）分成3个数，所以和我们之前讨论的4个苹果分给3个小朋友的问题是完全一致的，只是需要注意每个数是有可能分到0个2或5的，需要“借苹果”。

（2）从“分”变成“取”

例如2016年APMOPS第19题：

How many 10-digitwhole numbers are there, where in each number, the product of the 10 digits is 2 to the power of 27 ?

这道题目的乍一看可以用插板法解决——将27个2分给10个digit，但仔细一想会发现问题，因为对于1个digit来讲，最多只能分2的3次方，如果再多，此digit就会超过9。很显然在27个2随意分配时并不能达成上述要求，所以这道题目的做法需要转化一下，先将每个digit都放3个2，也就是8，此时共有30个2，所以我们需要从10个digit中一共取走3个2，剩下的就是27个2. 取这3个2的过程就相对于3个苹果分给10个小朋友（分到几个苹果就代表从这个digit取走几个2），每个digit最少取0个2，这样就可以用插板法解决问题。

（3）从“计数题”变成“方程题”

有时插板法这类计数问题会摇身一变，变成不定方程的形式，如2017年APMOPS第15题：

15. If x, y, z are all positive integers, find the number of solutions tothe equation x+y+z=7

Note that order of unknowns is important. For example, （x= 1, y= 5, z= 1）and（x= 1, y= 1, z= 5） are considered two differentsolutions.

这道题目看上去是以方程的形式存在，其实它可以看成就是将7个苹果分给x、y、z三位小朋友，从而用插板法解决问题。

（4）从限制条件相同变成限制条件不同

上述我们见到的题目都是每位拿到苹果的小朋友都要求至少拿1、至少拿0或者其他任意数，限制的条件是相同的，但某些题目并不是这样，例如：

How manynumbers between 2000 and 9999 have a digit sum equal to 10?

这道题相当于把10个苹果分给4个数位，分几个苹果就代表这个数位是几。但是在分时我们会发现限制条件不同：千位至少为2，但另外3个digit可以为0。所以我们需要分开做调整，可以先考虑千位至少为2，拿我们需要先给千位1个苹果，另外3个digit可以为0，所以我们需要再借3个苹果，一人分他们一个，所以相当于是一共10-1+3 = 12个苹果，分给4个digit，每个digit至少为1，从而解决了这个问题。

以上4种是APMOPS中常见的4种变形，大家需要认真掌握。插板法是我们在上周的《如何备考明年RMO和APMOPS》的讲座中为大家概括的四种常用方法之一，考虑到线下讲座名额有限，为了帮助更多的学生以及家长，讲座会再根据家长们的需求来新开场次，上周六没抢到名额的家长可以联系崔老师登记需求，新开讲座后会第一时间通知大家。

崔老师联系方式：WhatsApp：89417447，Wechat：13156530509