|
|
期待已久,终于和新加坡的小朋友见面了,上周我们大概测试了20多名同学,在整个测试过程中遇到的小朋友都是整个新加坡比较高端的的学生,让我印象深刻。同时在整个测试过程中我们也发现小朋友一些共同的学习问题,我们这里专门梳理一下,同时也结合我的经验来给大家一些学习的建议。
1、常见问题一:数感的缺失。
在数学的学习中,对于数字的感觉非常重要。我举几个比较常见的例子,看到91,立刻脑中应该浮现这不是一个 primer number,hence 91=13*7。看到111也是一样,应该马上知道111=3*37.等等等等。同时对于2的乘方也应该很熟悉,例如:2^2=4,2^5=32,2^10=1024等等。这样在很多时候,计算题和找规律的题目中,会有很大的优势。我们看一个例子:
找规律
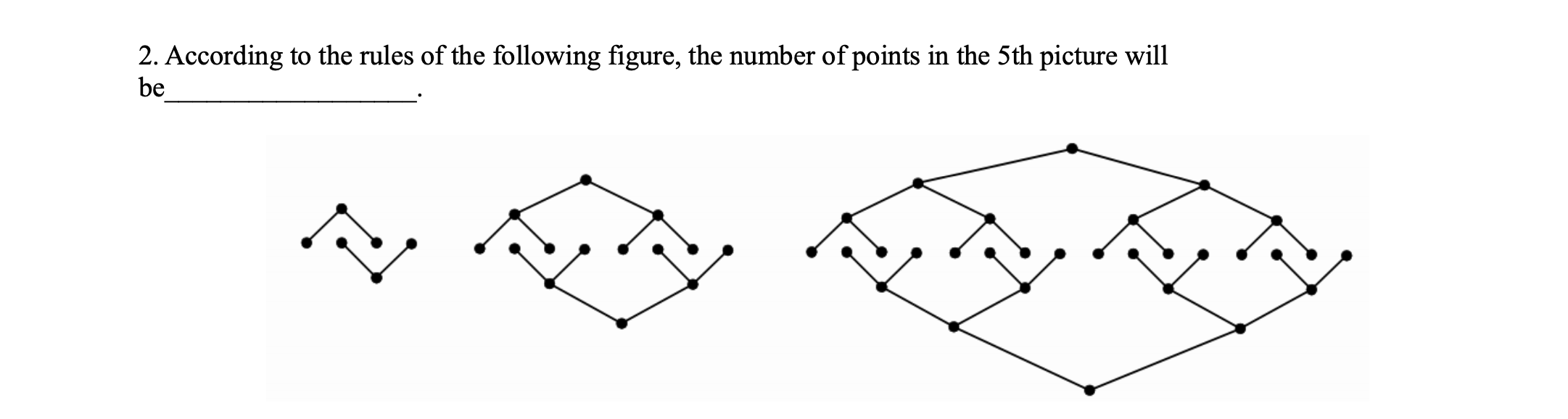
这是一个p6的题目,这一类的题目在psle和各类竞赛中都是经常考到的。这个题目也比较容易,基本上属于送分题一类。但是还是有不少小朋友会做错。当然做对的同学也很多。不过这个题目问的是第5个图形,如果我们把题目拓展一下到第100个,这个题目就有点难了。
我们可以看到图形与点的数量有以下的对应关系;
第一个:6
第二个:14
第三个:30
……这种情况下,其实规律是比较难以发现的。
当然,如果你有我说的数感,这一类题目其实都比较简单。因为我们有:
6=8-2=2^3-2;
14=16-2=2^4-2;
30=32-2=2^5-2;
我们就很容易可以看到其实第n个图形对应的点的数目是2^(n+2)-2;这样第100个图形的点数目是2^102-2。
那么这个题目当然还有其他很多方法来做,但是数感很好的同学用这个方法来做往往是简单的,快捷的。
2、常见问题2:机械使用公式。
公式是我们在数学学习中不可避免要遇到的,而且和很多人的想法不一样,我认为公式的学习在数学中是非常重要的,因为它可以大大简化我们解决问题的速度。但是学习公式最害怕的是,只会用公式,但不知道为什么用这个公式,以及这个公式是怎么来的一无所知。还有些学生,用公式解决问题的时候,非常的机械,这就让公式的学习反倒阻碍了数学能力的提升。我们再看一个例子。
等差数列

这个题目,有个同学的做法我大概简述如下:
s=2+4+6……60+62+64=2(1+2+3+……+30+31+32)=2(32+1)*32/2=33*32=1056.
当然大家可以看到,他是把所有的偶数全部除以2然后变成自然数再去求和。然后利用公式1+2+3+……+(n-1)+n=n(n+1)/2这个公式来计算。这样做当然不错。但是这样做,说明这个同学只知道自然数求和的公式,但不知道背后的原因。为什么这么说,自然数求和和偶数的求和本质上都是等差数列的求和,如果真的理解了这一点,就不会需要进行如此的变换。所以这时候就算是会使用自然数求和的公式,其实也不算是真的掌握了。
那么这一类题目应该怎么做,我觉得学生要明白等差数列求和的本质,虽然我们可以不一定要告诉学生这叫做等差数列这个名词,但是这个本质要搞清楚:
s=2+4+6……60+62+64;
然后我们把s里面每个数字倒序写一遍:
s=64+62+60+……+6+4+2;
这样两个s和在一起对齐写就会发现:
s=2 + 4 +6…… 60 + 62 + 64;
s=64 +62 +60+……+6 + 4 + 2;
在第一个位置两个数2+64=66;
在第二个位置两个数4+62=66;
在第三个位置两个数6+60=66;
以此类推:
就出现了很多个66,那么总共是多少个呢?原来这个序列有多少个数字,就有多少个66,这里是32个,那么:
2s=32*66;s=32*66/2=1056。
然后我们回过头来看,我们可以倒叙相加的原因是什么?是因为倒叙之后,相同位置两个数加起来是相等的,那为什么会这样?是因为这个序列的每个数和前一个数的差都相等,都是2.
于是我们可以总结一个规律这类题都是这样做:
当一个序列里,每个数和前一个数和都相同,那么求和就可以倒叙写一遍,然后相加:
s=(第一个数+最后一个数)*数字的个数/2.
以上是一个比较常见的例子,目的是要告诉大家,学习一个公式至少要会三件事:
1)明白这个公式使用的条件。
2)明白这个公式的来源和推导。
3)会在具体的情况下使用这个公式。
3、常见问题三:轻易使用方程。
方程是我们之后数学学习的基础,在数学,物理,化学等等科学类学科里,方程都是非常重要的。很多小朋友看到应用题和行程类的问题,脑子第一反应就是列一个方程来解决。这也是很多家长在辅导孩子的时候经常做的事情。这样做当然可以解决问题(解方程不要解错的前提下)。当然在小学奥数学习中,不是说不可以使用方程,很多时候有些题目可能只有方程做起来才比较容易。但是我们是不倡导使用方程的。原因是,一方面是列方程主要是要找等量关系,找到了等量关系问题就基本上可以解决。但是这样做会屏蔽掉很多分析问题的细节,而分析问题的能力才是小学应用题要培养的孩子的重要能力,这个能力是以后数学和科学学习的基础。这也是正是奥数学习的一大好处。第二个是很多题目往往用方程做的时候会比较复杂,解方程的过程会涉及到大量的计算,还有可能用小数和分数,那就增加了出错的概率。我们来看一个例子:
盈亏问题

这是道NMOS 2018年R1的考试题。这个题目如果用方程自然是可以做的,那么解法如下(我们只设一个未知数来解决):
我们假设:
the number of pupils is x,then
5x+4=6(x-3)+4;
we have x=18. the number of candies = 5*18+4=94.
这样做当然没有问题,但是就如我上面所说,其实孩子没有学习到很多分析问题的能力,我们换一个思路来看看,我们画个图来帮助思考:
situation 1: 5 5 5 …… 5 5 5 5 5 extra 4 candies
situation 2: 6 6 6 …… 6 6 extra 4 candies
从上面的图我们可以看到,除了在第2个情况下有3个缺席的暂时不用考虑。我们先考虑没有缺席的小朋友,就会发现,每个小朋友比第1种情况多拿到1 candy;而situation 1和situation 2的candies是一样多的。所以其实每个小朋友多拿到的1个candy就是来自3个未出席的小朋友,这3个小朋友原本每人应该有5个,这3人没有出现,所以其实会多出3*5=15个。而在situation 2 就是把这15个都分给没有缺席的小朋友每个人1个。这样我们很容易可以看出来,在situation 2出席的小朋友是15个。
也就是说,总共的 number of candies = 15*6+4=94.
这样做看起来要分析一大段,但其实背后的原理很简单。想清楚了,可以更快的做出题目,思路也更清晰,并且还能感觉到一种思维的乐趣,进一步增加学习的兴趣。
|
|