本帖最后由 张涛老师 于 2023-6-20 10:42 编辑
在上一篇帖子GEP备考之应用题模块分析中,我们详细的介绍了GEP数学的应用题模块。
除了应用题之外,最重要的就是几何模块。几何模块是二轮加入的考点,由此可见几何模块的重要性和难度。下面结合实例我们分析一下几何模块如何备考!
一、周长
GEP二轮只涉及长方形和正方形的周长:
①长方形的周长=(长+宽)×2. ②正方形的周长=边长×4. 考试中实际也是以考察周长公式为主,我们看下面这个例子: A square of perimeter 48 cm is cut into 2 pieces to make a rectangle (see the picture): What is the perimeter of the rectangle? 可以看到,这题考察了正方形、长方形的周长,常规做法是根据正方形周长求边长,再找长方形的长和宽;更快的做法可以直接找周长增加的部分,相当于增加了1条边长。整体来说难度不大,但要求同学们对基本知识点很熟练。
除此之外,也会有比较复杂的考察,比如不规则图形的周长问题: 本质上仍然是考察长方形和正方形的周长,但是需要同学们利用图形变换来进行转化:分别向下和向左平移两条较短线段,把不规则图形转化为正方形。
二、面积 GEP二轮数学对于面积的考察同样是基于正方形和长方形,但难度更大、综合度更高。 1.会考察不规则图形面积: 通常可以考虑利用图形变换,把不规则图形变成规则图形,上题有两种思路: (1)通过分割图形,把不规则图形变成两个长方形,可以分别算出面积再相加: (2)通过整体减空白: 把原图补成一个长方形,再减去多算的部分(正方形)。
2.会结合周长综合考察: 这一题需要同学们通过画图,搞清楚增加边的长度对于面积具体有什么影响。
3.会考察三角形面积: There was a square with 2 diagonals crossed at the centre of the square.The length of each diagonal of the square was 8 cm.Find the area of the square. 现阶段同学们还没有学过勾股定理,没办法通过正方形对角线求正方形边长,所以只能利用三角形面积公式,把正方形沿着对角线分割成两个大的三角形。 而三角形的面积怎么来的呢? 把两个相同三角形拼在一起,就是一个平行四边形,所以三角形面积是这个平行四边形的一半。所以还得搞清楚平行四边形的面积怎么求。 通过分割、平移,可以把平行四边形变成长方形,这样一来就可以得到平行四边形面积公式(底×高),进一步得到三角形面积公式(底×高÷2)。
4.会结合分数考察: GEP二轮数学的经典题型,求阴影部分面积是整个图的几分之几。这类题目难度较大,同学们不仅要学过三角形面积,还得学过等积变形(指改变形状而面积不变)和一半模型(指阴影部分占整个图形面积一半) 等积变形:
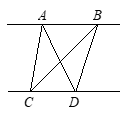
在平行线AB和CD之间,三角形ACD和三角形BCD面积一样,因为底相同,高相等(平行线间的距离处处相等)。
一半模型:

阴影部分面积是平行四边形的一半。所以上题中的蓝色部分,就是1/3的一半,也就是1/6.
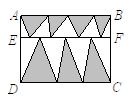
阴影部分面积是长方形的一半。可以把整个长方形分成若干个小的长方形,每块阴影是每个长方形的一半,各部分都是一半,加起来也是整体的一半。所以上述的第二题,阴影部分就是4/5的一半,也就是2/5.
今天关于GEP几何模块的分享就到这里了,文中涉及的题目也都整理如下。各位家长一定要记得给孩子们看看哦!如果家长或孩子们有什么问题,也欢迎随时在评论区提出!我看到就会立马回复的哦~
|